Data Science Using R ‘Value Added’ (Assignment 3)

Question 1.What is One-Way ANOVA test? How One-Way ANOVA test works?

The one-way analysis of variance (ANOVA), also known as one-factor ANOVA, is an extension of independent two-samples t-test for comparing means in a situation where there are more than two groups.

In one-way ANOVA, the data is organized into several groups base on one single grouping variable (also called factor variable). This tutorial describes the basic principle of the one-way ANOVA test and provides practical anova test examples in R software.

How it Works:

The one-way ANOVA compares the means between the groups you are interested in and determines whether any of those means are statistically significantly different from each other. Specifically, it tests the null hypothesis:

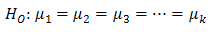
where µ = group mean and k = number of groups. If, however, the one-way ANOVA returns a statistically significant result, we accept the alternative hypothesis (H_A), which is that there are at least two group means that are statistically significantly different from each other.

Question 2: Suppose a grocery store sells “16 ounce” boxes of Captain Crisp cereal. A random
sample of 9 boxes was taken and weighed. The weight in ounces is stored in the data
frame capt_crisp.
capt_crisp = data.frame(weight = c(15.5, 16.2, 16.1, 15.8, 15.6, 16.0, 15.8, 15.9, 16.2))
The company that makes Captain Crisp cereal claims that the average weight of a box
is at least 16 ounces. We will assume the weight of cereal in a box is normally
distributed and use a 0.05 level of significance to test the company’s claim.

a) Write a command in R to calculate sample mean and sample standard deviation

>capt_crisp = data.frame(weight = c(15.5, 16.2, 16.1, 15.8, 15.6, 16.0, 15.8, 15.9, 16.2))
>print(mean(capt_crisp$weight))
Expected Output
[1][15.9]



>print(sqrt(var(capt_crisp$weight)))
Expected Output
[1][0.25]

b) Perform a one-sample t-test considering mu=16

>t.test(capt_crisp$weight,mu=16)

Expected Output

data: capt_crisp$weight
t = -1.2, df = 8, p-value = 0.2645
alternative hypothesis: true mean is not equal to 16
95 percent confidence interval:
15.70783 16.09217
sample estimates:
mean of x
15.9

c) Based on the p-value of the test depicts whether the null hypothesis will be
accepted or rejected?

Since the p-value we got from the one-sample t-test is 0.2645 which is greater than the
significance value of 0.05 so we fail to reject the null hypothesis.

---

Question 3: Since the p-value we got from the one-sample t-test is 0.2645 which is greater than the significance value of 0.05 so we fail to reject the null hypothesis.Perform Chi-square test to check if the two rows (Seat Belt Yes and Seat Belt No ) areindependent to each other?
Hints :

1. Convert two rows into a dataframe

2. A p-value smaller than significance level denotes dependency

Consider the following data on the severity of a crash tabulated for the cases where the
passenger had a seat belt, or did not:

seatbeltsyes = data. frame(seatbelts_yes=c(12813,647,359,42))
SeatbeltsNo = data. frame(Seatbelts_no=c(65963 ,4000, 2642, 303))

chisq.test(SeatbeltsvesSseatbelts_yes)
chisq.test(SeatbeltsNo$Seatbelts_no)

Expected Output
chi-squared test for given probabilities

data: seatbeltsyes$seatbelts_yes
X-squared = 33674, df = 3, p-value < 2.2e-16

> chisq. test (seatbeltsnoSseatbelts_no)

chi-squared test for given probabilities

data: SeatbeltsNoSseatbelts_no
X-squared = 167076, df = 3, p-value < 2.2e-16




Hence, Both the p-values are nearly = to 0 , both the rows are dependent on each other.

---

Question 4: Explain with an example measure of central tendency and measure of variance.

Central tendency is a descriptive summary of a dataset through a single value that reflects
the center of the data distribution. Central tendency performs the following measures:

Arithmetic Mean
Geometric Mean
Harmonic Mean
Mode
Median
A measure of variability is a summary statistic that represents the amount of dispersion in a
dataset. Following are some of the measures of variability that R offers to differentiate
between data sets:
Variance
Standard Deviation
Range
Mean Deviation
Interquartile Range

---

Question 5 : Write commands in R to pull tweets from twitter, convert unstructured tweets to
structured tweets i.r remove http, stop words etc.

Start R and download the package “rtweet”, which I will use to extract the tweets.

install.packages("rtweet")
library (rtweet)

Library and Commands Used for Cleaning the data.

        library(tidyverse)

        clean_tweets <- function(x) {
                    x %>%
                            # Remove URLs
                            str_remove_all(" ?(f|ht)(tp)(s?)(://)(.*)[.|/](.*)") %>%
                            # Remove mentions e.g. "@my_account"
                            str_remove_all("@[[:alnum:]_]{4,}") %>%
                            # Remove hashtags
                            str_remove_all("#[[:alnum:]_]+") %>%
                            # Replace "&" character reference with "and"
                            str_replace_all("&amp;", "and") %>%
                            # Remove puntucation, using a standard character class
                            str_remove_all("[[:punct:]]") %>%
                            # Remove "RT: " from beginning of retweets
                            str_remove_all("^RT:? ") %>%
                            # Replace any newline characters with a space
                            str_replace_all("\\\n", " ") %>%
                            # Make everything lowercase
                            str_to_lower() %>%
                            # Remove any trailing whitespace around the text
                            str_trim("both")
            }

        tweets %>% clean_tweets

---