An Introduction to Artificial Intelligence | Week 6
Session: JAN-APR 2024
Course name: An Introduction to Artificial Intelligence
Course Link: Click Here
For answers or latest updates join our telegram channel: Click here to join
These are An Introduction to Artificial Intelligence Answers Week 6
Q1. Select the CORRECT statements –
We can use Forward Checking to decide which variable we should assign next.
Tree-structured CSP can be solved in O(n2d) time.
Local Search is faster than Systematic Search for large values of n in n-Queens Problem.
The critical ratio is defined as (number of variables) / (number of constraints).
Answer: Local Search is faster than Systematic Search for large values of n in n-Queens Problem.
Q2. The time complexity of AC-3 algorithm and that of solving nearly tree-structured CSPs using cutset conditioning are, respectively, – (c is the size of cutset)
O(n2d2), O((n-c).dc+2)
O(n2d2), O((n-c).dc-2)
O(n2d3), O((n-c).dc+2)
O(n2d3), O((n-c).dc-2)
Answer: O(n2d3), O((n-c).dc+2)
For answers or latest updates join our telegram channel: Click here to join
These are An Introduction to Artificial Intelligence Answers Week 6
Q3. According to the heuristics discussed in the videos, which region should be colored first? (If there is a tie between regions, choose the region with the least label number)
Answer: 6
Q4. Suppose we assign Green to the region identified in the previous question. Let x be the label number of the region that we should color next. Let y be the number of colors we can assign to it. What is 4x+3y?
Answer: 14
For answers or latest updates join our telegram channel: Click here to join
These are An Introduction to Artificial Intelligence Answers Week 6
Q5. Consider that we first color Region 1 with Purple and want to color Region 6 next. Which of the following color (s) should we use?
Purple
Green
Yellow
We can’t use any colour
Answer: Purple
Q6. Which of the following is/are true ?
Arc Consistency can detect all failures
Tree-structured CSPs can be solved purely by inference
Arc Consistency helps propagate information between un-assigned variables
Tree-structured CSPs can be solved in polynomial time
Answer: b, c, d
For answers or latest updates join our telegram channel: Click here to join
These are An Introduction to Artificial Intelligence Answers Week 6
Q7. Which of the following is/are false for the standard search formulation for solving CSPs? Here, n is the number of variables, and d is the number of values in the domain of each variable. At every step, we branch by assigning a value to some unassigned variable.
At depth k, each node has d(n-k) children
All solutions are found at the same depth
The number of leaves in the tree is dn
Iterative deepening depth-first search is the best algorithm to perform the search on the resulting formulation
Answer: c, d
Q8. Which of the following heuristics/techniques will help speed up back-tracking search in practice?
Decomposing the original problem into independent sub-problems by finding connected components in the constraint graph and applying backing tracking search independently to each connected component
Assigning values to variables with the most number of legal values remaining first
Using arc-consistency to detect failures early
Picking the least constraining value of the variable chosen for assignment
Answer: a, c, d
For answers or latest updates join our telegram channel: Click here to join
These are An Introduction to Artificial Intelligence Answers Week 6
Q9. (True/False) Consider the following constraint graph, where nodes represent variables, edges represent constraints between them and the domains of each variable are indicated using the set notation. If we perform arc-consistency on this constraint graph, then we will be able to detect that no solution is possible.
True
False
Answer: True
Q10. Which of the following is true for solving CSPs with hill climbing using the min-conflicts heuristic
It can solve almost any randomly generated CSP in near constant time and is the most effective when the ratio between the number of constraints to the number of variables is close to the critical ratio
After selecting a conflicted variable for moving to a neighboring state, we choose the value of the variable that violates the minimum number of constraints
The objective function we try to minimize is the number of constraints violated
After selecting a conflicted variable for moving to a neighboring state, we choose the value of the variable that satisfies the most constraints
Answer: b, c
For answers or latest updates join our telegram channel: Click here to join
These are An Introduction to Artificial Intelligence Answers Week 6
More Weeks of An Introduction to Artificial Intelligence: Click here
More Nptel Courses: https://progiez.com/nptel-assignment-answers
Course Name: An Introduction to Artificial Intelligence
Course Link: Click Here
These are An Introduction to Artificial Intelligence Answers Week 6
Q1. Which of the following is true in the context of the standard search formulation of CSPs?
(there are n variables, each of which can take d values, at every step you branch by assigning a value to some unassigned variable)
a. All solutions appear at the same depth in the search tree
b. There are dn leaf nodes in the search tree, one for each possible assignment of values to the variables
c. There are n!dn leaf nodes in the search tree, n! for each possible assignment of values to the variables
d. Iterative deepening depth first search is the best algorithm to perform the search on the resulting formulation
Answer: a, c
These are An Introduction to Artificial Intelligence Answers Week 6
Q2. What is the worst-case time complexity of solving a CSP containing nk variables, each of which can take d values, if it is known that the problem can be decomposed into k independent subproblems, each containing n variables?
a. O(dnk2)
b. O(dnk)
c. O(kdn)
d. O((d/k)n)
Answer: c. O(kdn)
These are An Introduction to Artificial Intelligence Answers Week 6
Q3. Which of the following methods are unlikely to increase the speed of backtracking search for solving a CSP?
a. Cutset conditioning on a complete (fully connected) CSP graph.
b. Selecting variable with fewest legal values remaining
c. Using arc consistency to detect failures early
d. Selecting the most constraining value for a variable
Answer: a, c
These are An Introduction to Artificial Intelligence Answers Week 6
Q4. In which of the following settings is hill-climbing using min-conflicts heuristic likely to struggle the most?
a. Low number of constraints, low number of variables
b. Number of constraints >> Number of variables
c. Number of constraints << Number of variables
d. Near the critical ratio between number of constraints and number of variables
Answer: d. Near the critical ratio between number of constraints and number of variables
These are An Introduction to Artificial Intelligence Answers Week 6
Q5. Which of the following is true about arc consistency as a method to improve backtracking search based constraint satisfaction algorithms?
a. It helps in detecting failures early by leveraging constraints involving unassigned variables.
b. Arc consistency updates the domain of unassigned variables given the current assignment and detects failure when all the modified domains are empty
c. Arc-consistency can be performed in polynomial time.
d. Backtracking search with arc consistency and forward checking solves CSPs in polynomial time
Answer: a, c
These are An Introduction to Artificial Intelligence Answers Week 6
Q6. Consider the constraint graph given below. Each node can take values from the set {‘a’, ‘b’, ‘c’} and the constraints are that the variables connected by an edge in the constraint graph need to have different values. We will use the following CSP solving heuristics over backtracking searching with forward checking to find a satisfying assignment for the constraints.
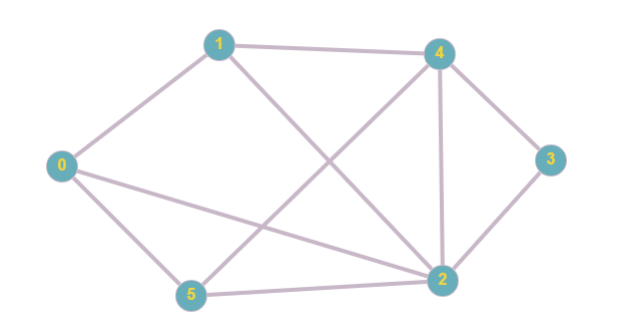
These are An Introduction to Artificial Intelligence Answers Week 6
I. For selecting which node to assign, select the numerically smallest unassigned node.
II. For assigning value to the node, select the smallest value possible in the current domain(as determined by the forward checking algorithm).
Determine the sequence of nodes that are assigned/re-assigned one by one till a satisfiable solution is reached.
Answer: 0123345
These are An Introduction to Artificial Intelligence Answers Week 6
Q7. In the above problem, suppose that for assigning value to the node, instead of II, the Least Constraining Value Heuristic is used with ties broken in the alphabetical order.
Suppose that nodes x1 ,x2 ,… xk are assigned/re-assigned values v1 ,v2 ,… vk . Determine x1v1x2v2 … xkvk . For example, if the nodes 0,3,1,2,4,5 are assigned a, b, c, a, b, b respectively, the correct response will be 0a3b1c2a4b5b.
Answer: 0a1b2c3b4a5b
These are An Introduction to Artificial Intelligence Answers Week 6
Q8. In the above problem, the following additional unary constraints are added:
Value(0) = a
Value(1) = b
Value(2) = c
Suppose we enforce these constraints(assign 0,1 and 2 with corresponding values) and perform the arc-consistency algorithm AC-3, which of the following are correct about the modified domains of the unassigned variables?
a. Modified domain of variable 3, is {b}
b. Using the modified domains, the search terminates without ever backtracking, i.e without ever re-assigning any previously assigned variable with another value.
c. Modified domain of variable 3 is {a,b}
d. Using forward checking instead of AC-3 would have resulted in the same modified domains for this problem.
Answer: a, b
These are An Introduction to Artificial Intelligence Answers Week 6
Q9. For the constraint graph of problem 6, suppose we want to use cycle cutsets to modify it into a tree-shaped constraint graph. How many minimum nodes need to be removed in the process?
Answer: 2
These are An Introduction to Artificial Intelligence Answers Week 6
Q10. Consider constraint satisfaction problems with n variables and a domain of size d. Which of the following are correct regarding the worst case time complexity of algorithms for constraint satisfaction problems?
a. Using the minimum remaining values heuristic and the least constraining value heuristic reduces the worst case time complexity to polynomial in n and d.
b. Worst time complexity is O(nd) irrespective of heuristic.
c. If the minimum cycle cutset has size c, time complexity is O(ndc+2)
d. For a tree shaped constraint graph, time complexity is O(d)
Answer: c. If the minimum cycle cutset has size c, time complexity is O(ndc+2)
These are An Introduction to Artificial Intelligence Answers Week 6
More Solutions of An Introduction to Artificial Intelligence: Click Here
More NPTEL Solutions: https://progiez.com/nptel-assignment-answers/
