Programming Data Structure And Algorithms Using Python | Week 8
Session: JULY-DEC 2023
Course Name: Programming Data Structure And Algorithms Using Python
Course Link: Click Here
These are Programming Data Structure And Algorithms Assignment 8 Answers
Programming Assignment
Question
Dividing Sequences
(IARCS OPC Archive, K Narayan Kumar, CMI)
This problem is about sequences of positive integers a1,a2,…,aN. A subsequence of a sequence is anything obtained by dropping some of the elements. For example, 3,7,11,3 is a subsequence of 6,3,11,5,7,4,3,11,5,3 , but 3,3,7 is not a subsequence of 6,3,11,5,7,4,3,11,5,3 .
A fully dividing sequence is a sequence a1,a2,…,aN where ai divides aj whenever i < j. For example, 3,15,60,720 is a fully dividing sequence.
Given a sequence of integers your aim is to find the length of the longest fully dividing subsequence of this sequence.
Consider the sequence 2,3,7,8,14,39,145,76,320
It has a fully dividing sequence of length 3, namely 2,8,320, but none of length 4 or greater.
Consider the sequence 2,11,16,12,36,60,71,17,29,144,288,129,432,993 .
It has two fully dividing subsequences of length 5,
•2,11,16,12,36,60,71,17,29,144,288,129,432,993 and
•2,11,16,12,36,60,71,17,29,144,288,129,432,993
and none of length 6 or greater.
Solution:
n = int(input())
L = list()
bestvals =list()
best_stored = list()
for x in range(n):
L.append(int(input()))
best_stored.append(0)
best_stored[0] = 1
for i in range(n):
maxval = 1
for j in range(i):
if L[i] % L[j] == 0:
maxval = max(maxval,(best_stored[j])+1)
best_stored[i] = maxval
print(max(best_stored),end="")These are Programming Data Structure And Algorithms Assignment 8 Answers
More Weeks of Programming Data Structure And Algorithms Using Python: Click here
More Nptel Courses: Click here
Session: JAN-APR 2023
Course Name: Programming Data Structure And Algorithms Using Python
Course Link: Click Here
These are Programming Data Structure And Algorithms Assignment 8 Answers
Here there be Dragons
(IOI Training Camp, 2012)
The kingdom is falling into ruin. People live in fear. Dragons pillage, kill, and just generally cause as much havoc as they possibly can. The king has just sent out a royal decree:
To any man out there who is able to bring me the heads of K dragons, I shall bequeath a lordship–to him, his sons and his grandsons, till the end of time.
Having seen this royal decree, and knowing that you are capable of killing dragons thanks to your extensive medieval combat training, you set out on a quest to hunt down the evil creatures. Being a busy kind of guy, you would like to complete your quest quickly and kill K dragons through the shortest route.
The kingdom is arranged in a grid with R rows, numbered 0 to R-1, and C columns, numbered 0 to C-1 You start your quest at the top left corner of the grid, (0,0).
These are Programming Data Structure And Algorithms Assignment 8 Answers
The total number of dragons in the kingdom is D, of which you have to kill K. Dragons are very territorial in nature, so each row of the grid contains at most one dragon. Also, since the kingdom is situated on a hill, you travel only downwards on the grid, though you may move left or right as you please.
You are told that no two dragons are on the same row of the grid. Also, no dragon is at position (0,0).
For example, suppose the grid has 5 rows and 5 columns with 3 dragons, of which you have to kill any 2. The three dragons are located at (1,4), (2,3) and (4,4), as shown below. In this case, your shortest route is to take 7 steps and kill the dragons in row 1 and row 2. Killing any other combination of 2 dragons takes 8 steps, so this is the minimum possible. Note that once you’ve killed K dragons, you don’t incur any cost to return home. You just want to find how long it takes to do all the killing.
These are Programming Data Structure And Algorithms Assignment 8 Answers
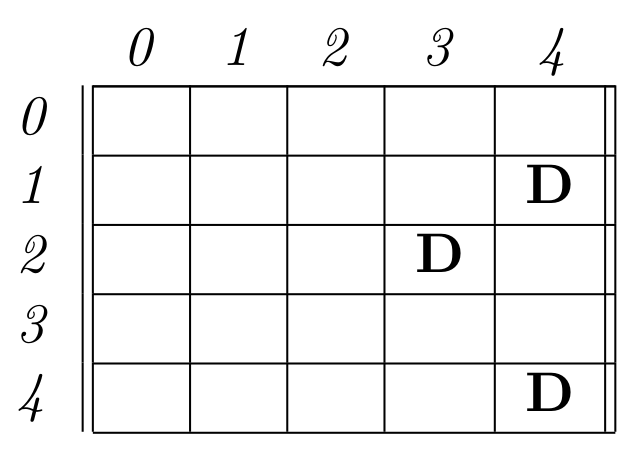
Solution hint
Number the dragons 1,2,…,D in ascending order of rows. Let mindist(i,j) denote the minimum distance travelled when the jth dragon killed is dragon i. Recall the constraint that there is no dragon at (0,0). Use dynamic programming to compute mindist(i,j) for all values of i and j, then find the minimum among mindist(i,K) for all i ≥ K.
These are Programming Data Structure And Algorithms Assignment 8 Answers
Input format
- Line 1 : Four space-separated integers, R, C, K and D.
- Lines 2 to D+1 : Each line has two-space separated integers r and c, the row and column of the corresponding dragon.
Output format
A single integer, the minimum total distance travelled to kill K dragons.
These are Programming Data Structure And Algorithms Assignment 8 Answers
Test Data:
- In all testcases, K ≤ D ≤ R, and, for each dragon position (r,c), 0 ≤ r < R, and 0 ≤ c < C.
- In all testcases, 1 ≤ K,D ≤ 300.
- In 60% of the testcases, 1 ≤ R,C ≤ 300. In the remaining testcases, 1 ≤ R,C ≤ 100000.
- No two dragons will be on the same row.
- No dragon will be at position (0,0).
Sample Input:
5 5 2 3
1 4
4 4
2 3
Sample Output:
7
These are Programming Data Structure And Algorithms Assignment 8 Answers
import sys
INF = sys.maxsize
dist = [[0] * 350 for i in range(350)]
dp = [[0] * 350 for i in range(350)]
r, c, k, d = map(int, input().split())
a = [(0, 0)]
for i in range(d):
u, v = map(int, input().split())
a.append((u, v))
a.sort()
for i in range(1, d + 1):
for j in range(1, d + 1):
if not dist[i][j]:
dist[i][j] = dist[j][i] = abs(a[i][0] - a[j][0]) + abs(a[i][1] - a[j][1])
for i in range(1, d - k + 2):
dp[1][i] = a[i][0] + a[i][1]
for i in range(2, k + 1):
for j in range(i, d + 1):
temp = INF
for p in range(j - 1, 0, -1):
if dp[i - 1][p] and temp > dist[p][j] + dp[i - 1][p]:
temp = dist[p][j] + dp[i - 1][p]
dp[i][j] = temp
ans = INF
for i in range(k, d + 1):
ans = min(ans, dp[k][i])
print(ans)These are Programming Data Structure And Algorithms Assignment 8 Answers
More Weeks of Programming Data Structure And Algorithms: Click Here
More Nptel courses: https://progiez.com/nptel
Session: JULY-DEC 2022
Course Name: Programming Data Structure And Algorithms Using Python
Link of Course: Click Here
These are Programming Data Structure And Algorithms Assignment 8 Answers
Q1 Domino Solitaire
(Indian National Olympiad in Informatics, 2008)
In Domino Solitaire, you have a grid with two rows and many columns. Each square in the grid contains an integer. You are given a supply of rectangular 2 x 1 tiles, each of which exactly covers two adjacent squares of the grid. You have to place tiles to cover all the squares in the grid such that each tile covers two squares and no pair of tiles overlap.
These are Programming Data Structure And Algorithms Assignment 8 Answers
The score for a tile is the difference between the bigger and the smaller number that are covered by the tile. The aim of the game is to maximize the sum of the scores of all the tiles. Here is an example of a grid, along with two different tilings and their scores.
The score for Tiling 1 is 12 = (9-8)+(6-2)+(7-1)+(3-2) while the score for Tiling 2 is 6 = (8-6)+(9-7)+(3-2)+(2-1). There are other tilings possible for this grid, but you can check that Tiling 1 has the maximum score among all tilings. Your task is to read the grid of numbers and compute the maximum score that can be achieved by any tiling of the grid.
These are Programming Data Structure And Algorithms Assignment 8 Answers
Solution:
//CodeThese are Programming Data Structure And Algorithms Assignment 8 Answers
More NPTEL Solutions: https://progiez.com/nptel
