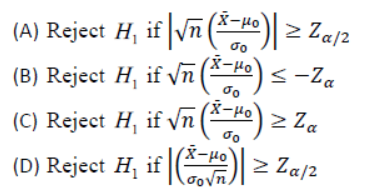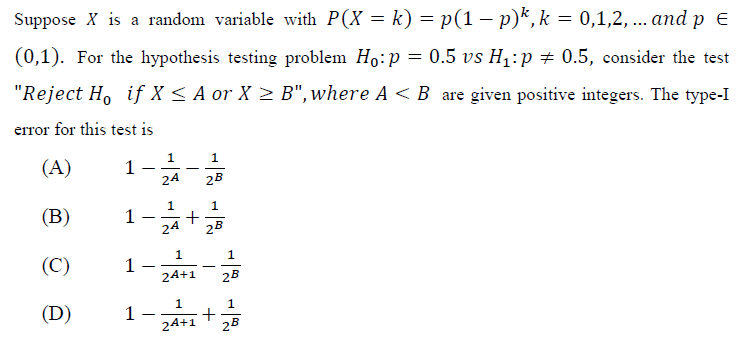Probability And Statistics | Week 9

Course Name: Probability And Statistics

Course Link: Click Here

These are Probability And Statistics Week 9 Assignment 9 Answers

---

Q1. Let X₁,…, X_m be a random sample from Poisson distribution with parameters λ, 0 < λ. Which of the following is an unbiased estimator of λ?
(A) X̅, S²
(B) X̅, S², αX̅ + (1 – α)S²; 0 ≤ a ≤1
(C) X̅
(D) S²

Answer: (B) X̅, S², αX̅ + (1 – α)S²; 0 ≤ a ≤1

---

Q2. Let three random samples of sizes n₁ = 20, n₂ = 10 and n₃ = 8 be taken from a population with mean μ and variance σ2. Then which of the following is an unbiased estimator of σ².
(A) S²₁
(B) S²₂
(C) S²₃
(D) 20S²₁+10S²₂+8S²₃/38

Answer: (D) 20S²₁+10S²₂+8S²₃/38

---

These are Probability And Statistics Week 9 Assignment 9 Answers

---

Q3. Let X₁,…, X_n be a random sample from a gamma population with parameters r and λ. Find the moment estimators of λ and r.
(A) X̅, X̅²
(B) 1/X̅, 1/X̅²
(C) X̅/(1/n)Σⁿ_i=1X²_i-X̅², X̅²/(1/n)Σⁿ_i=1X²_i-X̅²
(D) n-1/X̅, n-1/X̅²

Answer: (C) X̅/(1/n)Σⁿ_i=1X²_i-X̅², X̅²/(1/n)Σⁿ_i=1X²_i-X̅²

---

Q4. Let X₁,…, X_n be a random sample from N(0, 1), where θ > 0. Find the MLE of θ.
(A) X̅
(B) 1/X̅
(C) X̅²
(D) 2X̅

Answer: (A) X̅

---

These are Probability And Statistics Week 9 Assignment 9 Answers

---

Q5. Let X₁,…, X_n be a random sample from exponential distribution with mean μ. Find the MSE of an estimator T = 1/n+1Σⁿ_i=X_i of μ.
(A) µ²
(B) μ²/n+1
(C) μ²/n(n+1)
(D) nμ²/n+1

Answer: (B) μ²/n+1

---

Q6. Let X be a Bernoulli random variable with P(X = 1) = p and P(X = 0) = 1-p, 0 < p < 1. If μ_n denotes the nth moment about mean and μ_2n+1 = 0 iff
(A) p = 1/4
(B) p = 1/3
(C) p = 1/2
(D) p = 2/3

Answer: (C) p = 1/2

---

These are Probability And Statistics Week 9 Assignment 9 Answers

---

Q7. Let X₁,…, X_n be iid random variables with EX_i = μ and E|X_i|² < ∞. Which among the following is a consistent estimator for μ?
(A) (Πⁿ_i=1/X_i)¹^/n
(B) 2X̅
(C) X₍₁₎
(D) 2[n(n+1)]^-1Σⁿ_i=1iX_i

Answer: (D) 2[n(n+1)]^-1Σⁿ_i=1iX_i

---

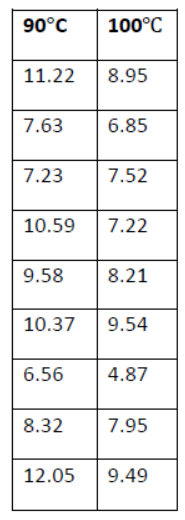
Q8. Let -2,-6,5,9,-5,-9 be the observed values of a random sample of size 6 from population having density function given by
f_θ(x) = e^-(x-θ), x > θ
Then MLE of θ is
(A) -9
(B) 9
(C) 4/3
(D) -4/3

Answer: (A) -9

---

These are Probability And Statistics Week 9 Assignment 9 Answers

---

Q9.

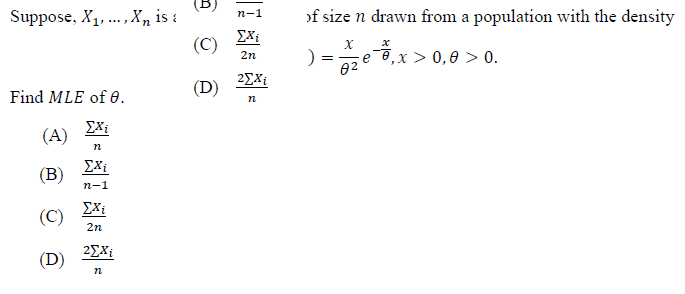
Answer: (C)

---

Q10. Let X₁,……. Xn be a random sample from U(1,θ) population, where θ > 1. If X_(n) = max (X₁, …, X_n), then which of the following is an unbiased estimator of θ ?
(A) n+1/n X_(n) +1/n
(B) n+1/n X_(n) -2/n
(C) 2X̅ – 1
(D) n/n+1 X_(n) + 1/n

Answer: (C) 2X̅ – 1

---

These are Probability And Statistics Week 9 Assignment 9 Answers

More Weeks of Probability and Statistics: Click Here

More Nptel courses: https://progiez.com/nptel

---

---

These are Probability And Statistics Week 9 Assignment 9 Answers

---