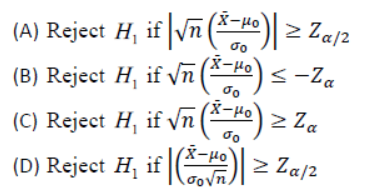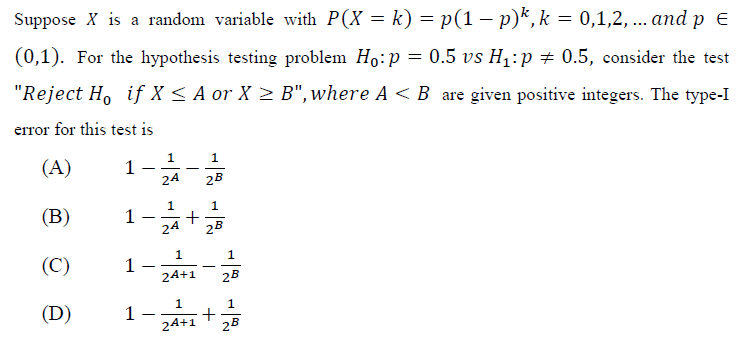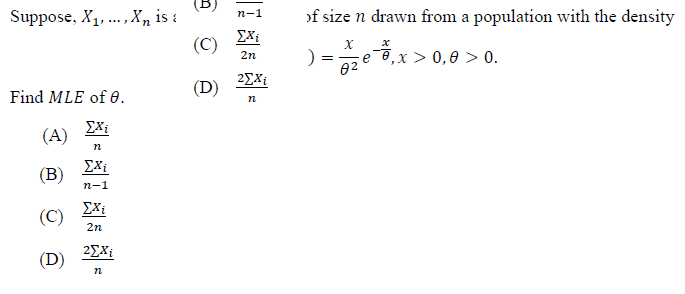Probability And Statistics | Week 7

Course Name: Probability And Statistics

Course Link: Click Here

These are Probability And Statistics Week 7 Assignment 7 Answers

---

Q1. Let X₁, X₁, X3 and X4 be independent random variables with respective means 1,1/2,1/3,1/4. Then Y = min(X₁, X₂, X3, X4) has an exponential distribution with the mean equal to
(A) 0.1
(B) 0.48
(C) 2.08
(D) 0.5

Answer: (A) 0.1

---

Q2. Test results from an electronic circuit board indicate that 50% of board failures are caused by assembly defects, 40% are due to electrical components and 10% are due to mechanical defects. Suppose that 10 boards fail independently. Let the random variables X, Y and Z denote the number of assembly, electrical and mechanical defects among the 10 boards. Calculate P(X= 5, Y = 3, Z = 2).
(A) 0.0602
(B) 0.0504
(C) 0.0204
(D) 0.0806

Answer: (C) 0.0204

---

These are Probability And Statistics Week 7 Assignment 7 Answers

---

Q3. Soft drink cans are filled by an automated filling machine. Assume that the fill volumes of the cans are independent, normal random variables with the standard deviation 15mL. Suppose the probability that the mean of a sample of 100 cans is below 350mL is 0.005. What should the mean fill volume be equal to?
(A) 258.369
(B) 353.8637
(C) 360.257
(D) 257.952

Answer: (B) 353.8637

---

Q4. A plastic casing for a magnetic disk is composed of two halves. The thickness of each half is normally distributed with a mean of 2 millimeters and a standard deviation of 0.1 millimeter and the two halves are independent. What is the probability that the total thickness exceeds 4.3 millimeters?
(A) 0.01695
(B) 0.04962
(C) 0.02032
(D) 0.07081

Answer: (A) 0.01695

---

These are Probability And Statistics Week 7 Assignment 7 Answers

---

Q5. The joint density function of continuous random variables X and Y is given by
f(x,y) = {x + y, 0<x< 1,0 <y<1 0, otherwise
Let U=X-Y. Find Var (U)
(A) 1/4
(B) 1/6
(C) 1/18
(D) 1/3

Answer: (B) 1/6

---

Q6. Suppose that X₁, X₂, …, Xn are random variables such that the variances of each variable are 1 and correlation between each pair of different variables is 1/4. Then Var (X₁ + X₂ + … + Xn) is?
(A) n(n+1)/2
(B) n(n+2)/4
(C) n(n+3)/4
(D) n(n+3)/2

Answer: (D) n(n+3)/2

---

These are Probability And Statistics Week 7 Assignment 7 Answers

---

Q7. The joint distribution of the continuous random variables X, Y and Z is constant over the region x² + y² ≤ 1,0 <z < 4. Determine marginal probability density function of X.
(A) 8x²,0 < x < 1
(B) π²√1 − x²,−1≤ x ≤ 1
(C) √1-x², -1 ≤ x ≤ 1
(D) x/2,-1/2≤x≤1/2

Answer: (B) π²√1 − x²,−1≤ x ≤ 1

---

Q8. X and Y be continuous random variables with the joint pdf
f_XY = {e^-y(1-e^-x), 0<x<y<∞ e^-x(1-e^-y), 0<y≤x<∞
Find E(X+Y).
(A) 1
(B) 2
(C) 4
(D) 6

Answer: (C) 4

---

These are Probability And Statistics Week 7 Assignment 7 Answers

---

Q9. Suppose X₁,…, X10 are iid random variables following an exponential distribution with the mean 9. Find P(Y> 7|Y > 4), where Y = min {X₁,…,X₁₀}
(A) 0.03579
(B) 0.09697
(C) 0.18888
(D) 0.01312

Answer: (A) 0.03579

---

Q10. Let X₁, X2, X3, X4 and X5 be iid with common pdf given by
f(x) = { 1, 0<x< 1 0, otherwise
Suppose pdf of X(3) is of the form g3 (y3) = Ay₃^B (1 – y₃); 0 < y₃ < 1. Then (A, B, C) is
(A) (30,2,2)
(B) (30,2,3)
(C) (15,2,2)
(D) (30,4,3)

Answer: (A) (30,2,2)

---

These are Probability And Statistics Week 7 Assignment 7 Answers

More Weeks of Probability and Statistics: Click Here

More Nptel courses: https://progiez.com/nptel

---

---

These are Probability And Statistics Week 7 Assignment 7 Answers

---