Deep Learning Week 2 Assignment Answers Nptel
In this post you will get NPTEL Deep Learning Week 2 Assignment 2 Answers and solution . All weeks solutions of this course available here. This page provides verified NPTEL Deep Learning Week 2 Assignment 2 Answers for the NPTEL January–April 2026 session on the SWAYAM platform. These solutions are intended to help students cross-check their answers, understand key blockchain concepts, and avoid mistakes before final submission.
Previous session answers (Jan–Apr 2025, Jan–Apr 2024, and Jan–Apr 2022) are archived below for reference only, while the current Jan–Apr 2026 answers are updated regularly.
Table of Contents
NPTEL Deep Learning Week 2 Assignment 2 Answers (Jan-Apr 2026)
Que.1
Why is the natural logarithm often applied to the discriminant function gᵢ(X) = P(X|ωᵢ)P(ωᵢ)?
a) To normalize the probability values between 0 and 1
b) To ensure the function remains monotonically decreasing
c) To convert multiplication of probabilities into a more computationally advantageous addition operation
d) To eliminate the need for calculating the mean vector
Que.2
What is the physical significance of a covariance matrix in the form Σᵢ = σ²I?
a) Feature components are statistically dependent with varying variances
b) Feature components are statistically independent and have the same variance
c) The distribution of points in the feature space is always hyper-ellipsoidal
d) The decision boundary must be quadratic
Que.3
Which of the following is true regarding functions of discriminant functions fᵢ(x), i.e., f(gᵢ(x))?
a) We cannot use functions of discriminant functions as discriminant functions for multiclass classification
b) We can use them only if they are constant functions
c) We can use them if they are monotonically increasing functions
d) None of the above
Que.4
Suppose you are solving a three-class problem, how many discriminant functions will you need?
a) 1
b) 2
c) 3
d) 4
Que.5
For a two-class problem, the linear discriminant function is given by g(x) = aᵀy. What is the update rule for finding the weight vector a?
a) a(k + 1) = a(k) + η∑y
b) a(k + 1) = a(k) − η∑y
c) a(k + 1) = a(k − 1) − ηa(k)
d) a(k + 1) = a(k − 1) + ηa(k)
Que.6
In a 2-class problem, assume the feature points are sampled from normal distribution and a Bayesian classifier is used. How does the decision boundary change if P(ω₁) > P(ω₂) while Σ₁ = Σ₂ = σ²I?
a) It remains an orthogonal bisector
b) It shifts towards the mean μ₁
c) It shifts towards the mean μ₂
d) It becomes quadratic
Que.7
What is the primary drawback of the Nearest Neighbour (NN) rule in large-scale machine learning applications?
a) Cannot handle non-linear decision boundaries
b) Always produces a linear classifier
c) Highly sensitive to covariance matrix
d) Requires storing all training vectors and heavy computation during testing
Que.8
Using KNN (K = 3) with Manhattan distance, classify points A = (6,11) and B = (14,3).
a) A → Class 1, B → Class 1
b) A → Class 2, B → Class 2
c) A → Class 1, B → Class 2
d) A → Class 2, B → Class 1
Que.9
Given μ₁ = [10, 5]ᵀ, μ₂ = [2, 1]ᵀ, σ² = 2, P(ω₁) = 0.8, P(ω₂) = 0.2. Where does the decision boundary intersect the line joining the means?
a) [6, 3]ᵀ
b) [6.3, 3.7]ᵀ
c) [1.5, 5.6]ᵀ
d) [5.7, 2.9]ᵀ
Que.10
The class conditional probability density function p(x|ωᵢ) for a multivariate Gaussian distribution is given by:
a) (1 / (2π)^(d/2)|Σᵢ|^(1/2)) exp(−1/2 (x − μᵢ)ᵀ Σᵢ⁻¹ (x − μᵢ))
b) (1 / (2π)^(d/2)) exp(−1/2 (x − μᵢ)ᵀ Σᵢ⁻¹ (x − μᵢ))
c) (1 / (2π)^(d/2)σ²) exp(−1/2 (x − μᵢ)ᵀ (x − μᵢ))
d) None of the above
(Jan-Apr 2025)
Course Link: Click Here
1. Suppose if you are solving an n-class problem, how many discriminant function you will need
for solving?
a. n-1
b. n
C. n+1
d. n2
- If we choose the discriminant function g;(x) as a function of posterior probability. i.e. g;(x) = f(p(w;/x)). Then which of following cannot be the function f( )?
a. f(x) =a*,wherea>1
b. f(x) =a™*,wherea>1
c f(x)=2x+3
d. f(x) =exp(x)
- What will be the nature of the decision surface when the covariance matrices of different classes are identical but otherwise arbitrary? (Given all the classes have equal class probabilities)
a. Always orthogonal to two surfaces
b. Generally not orthogonal to two surfaces
c. Bisector of the line joining two means, but not always orthogonal to two surfaces
d. Arbitrary
- The mean and variance of all the samples of two different normally distributed classes w1w_1 and w2w_2 are given. What will be the expression of the decision boundary between these two classes if both the classes have equal class probability 0.5? For the input sample xx, consider gt(x)=xg_t(x) = x
a.
b.
c
d
- For a two-class problem, the linear discriminant function is given by g(x)=aTyg(x) = a^T y. What is the updating rule for finding the weight vector aa? Here, yy is an augmented feature vector.
a. Adding the sum of all augmented feature vectors that are misclassified, multiplied by the learning rate, to the current weight vector
b. Subtracting the sum of all augmented feature vectors that are misclassified, multiplied by the learning rate, from the current weight vector
c. Adding the sum of all augmented feature vectors belonging to the positive class, multiplied by the learning rate, to the current weight vector
d. Subtracting the sum of all augmented feature vectors belonging to the negative class, multiplied by the learning rate, from the current weight vector
- For a minimum distance classifier, which of the following must be satisfied?
a. All the classes should have identical covariance matrix and diagonal matrix
b. All the classes should have identical covariance matrix but otherwise arbitrary
c. All the classes should have equal class probability
d. None of the above
- Which of the following is the updating rule of the gradient descent algorithm? Here, ∇\nabla is the gradient operator and η\eta is the learning rate.
a. an+1=an−η∇F(an)
b. an+1=an+η∇F(an)
c. an+1=an−η∇F(an−1)
d. an+1=an+ηa_(n-1)
- The decision surface between two normally distributed classes w1w_1 and w2w_2 is shown in the figure. Can you comment on which of the following is true?
a. —
b. —
c. —
d. None of the above
- In k-nearest neighbors algorithm (k-NN), how do we classify an unknown object?
a. Assigning the label which is most frequent among the k nearest training samples
b. Assigning the unknown object to the class of its nearest neighbor among training samples
c. Assigning the label which is most frequent among all training samples except the k farthest neighbors
d. None of the above
- What is the direction of the weight vector ww with respect to the decision surface for a linear classifier?
a. Parallel
b. Normal
c. At an inclination of 45°
d. Arbitrary
NPTEL Deep Learning Week 2 Assignment 2 Answers 2023
Q1. Suppose if you are solving a four class problem, how many discriminant function you will need for solving?
a. 1
b. 2
c. 3
d. 4
Answer: d. 4
Q2. Two random variable X1 and X2 follows Gaussian distribution with following mean and covariance.
X1~N (0, 3) and X2~N (0, 2).
Which of following will is true.
a. Distribution of X1 will be more flat than the distribution of X2.
b. Distribution of X2 will be more flat than the distribution of X1.
c. Peak of the both distribution will be same
d. None of above.
Answer: a. Distribution of X1 will be more flat than the distribution of X2.
These are NPTEL Deep Learning Week 2 Assignment 2 Answers
Q3. Which of the following is true with respect to the discriminant function for normal density.\?
a. Decision surface is always orthogonal bisector to two surfaces when the covariance matrices of different classes are identical but otherwise arbitrary
b. Decision surface is generally not orthogonal to two surfaces when the covariance matrices of different classes are identical but otherwise arbitrary
c. Decision surface is always orthogonal to two surfaces but not bisector when the covariance matrices of different classes are identical but otherwise arbitrary
d. Decision surface is arbitrary when the covariance matrices of different classes are identical but otherwise arbitrary
Answer: b. Decision surface is generally not orthogonal to two surfaces when the covariance matrices of different classes are identical but otherwise arbitrary
Q4. In which of following case the decision surface intersect the line joining two means of two class at midpoint? (Consider class variance is large relative to the difference of two means)
a. When both the covariance matrices are identical and diagonal matrix.
b. When the covariance matrices for both the class are identical but otherwise arbitrary.
c. When both the covariance matrices are identical and diagonal matrix, and both the class has equal class probability.
d. When the covariance matrices for both class are arbitrary and different.
Answer: c. When both the covariance matrices are identical and diagonal matrix, and both the class has equal class probability.
These are NPTEL Deep Learning Week 2 Assignment 2 Answers
Q5. The decision surface between two normally distributed class w₁ and w2 is shown on the figure. Can you comment which of the following is true?
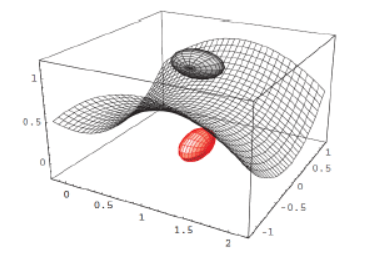
a. Σi = 621, where Σi is covariance matrix of class i
b. Σi = Σ, where Σ₁ is covariance matrix of class i
c. Σi = arbitary, where Σi is covariance matrix of class i
d. None of the above.
Answer: c. Σi = arbitary, where Σi is covariance matrix of class i
Q6. For minimum distance classifier which of the following must be satisfied?
a. All the classes should have identical covariance matrix and diagonal matrix.
b. All the classes should have identical covariance matrix but otherwise arbitrary.
c. All the classes should have equal class probability.
d. None of above.
Answer: c. All the classes should have equal class probability.
These are NPTEL Deep Learning Week 2 Assignment 2 Answers
Q7. You found your designed software for detecting spam mails has achieved an accuracy of 99%, i.e., it can detect 99% of the spam emails, and the false positive (a non-spam email detected as spam) probability turned out to be 5%. It is known that 50% of mails are spam mails. Now if an email is detected as spam, then what is the probability that it is in fact a non-spam email?
a. 5/104
b. 5/100
c. 4.9/100
d. 0.25/100
Answer: a. 5/104
These are NPTEL Deep Learning Week 2 Assignment 2 Answers
Q8. Which of the following statements are true with respect to K-NN classifier?
1. In case of very large value of k, we may include points from other classes into the neighbourhood.
2. In case of too small value of k the algorithm is very sensitive to noise.
3. KNN classifier classify unknown samples by assigning the label which is most frequent among the k nearest training samples.
a. Statement 1 only
b. Statement 1 and 2 only
c. Statement 1, 2, and 3
d. Statement 1 and 3 only
Answer: c. Statement 1, 2, and 3
These are NPTEL Deep Learning Week 2 Assignment 2 Answers
Q9. You have given the following 2 statements, find which of these option is/are true in case of k NN?
4. In case of very large value of k, we may include points from other classes into the neighbourhood.
5. In case of too small value of k the algorithm is very sensitive to noise.
a. 1
b. 2
c. 1 and 2
d. None of this.
Answer: c. 1 and 2
These are NPTEL Deep Learning Week 2 Assignment 2 Answers
Q10. The decision boundary of linear classifier is given by the following equation.
4x₁ + 6x₂ – 11 = 0
What will be class of the following two unknown input example? (Consider class 1 as positive class, and class 2 as the negative class)
a2= [1, 2]
a2= [1,1]
a. a1 belongs to class 1, a2 belongs to class 2
b. a2 belongs to class 1, a1 belongs to class 2 belongs to class 2
c. a1 belongs to class 2, a2 belongs to class 2
d. a1 belongs to class 1, a2 belongs to class 1
Answer: a. a1 belongs to class 1, a2 belongs to class 2
These are NPTEL Deep Learning Week 2 Assignment 2 Answers
These are NPTEL Deep Learning Week 2 Assignment 2 Answers
More weeks of Deep Learning: Click Here